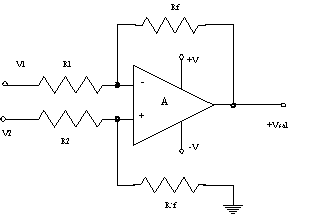
Se trata de una configuración con dos entradas, en la que se amplifica la diferencia de potencial entre ambas. Para obtener las expresiones correspondientes a esta configuración tendremos en cuenta que su comportamiento es en todo momento lineal. Por ello, aplicaremos el teorema de superposición. Primero supondremos que una de las tensiones de entrada es nula y obtendremos la salida correspondiente, a continuación supondremos que la otra tensión es nula y también obtendremos la expresión de Vo, la solución completa se consigue mediante la suma de ambas soluciones.
Analizamos el circuito por superposición dividiéndolo en los dos subcircuitos siguientes:
– Primer caso: V2=0:
En este caso al considerar que V2 es igual a cero obtenemos que R1 y R2 están en paralelo con lo cual el circuito tomaría la forma:
Sabemos que la intensidad I que atraviesa la resistencia equivalente debe ser nula, por lo que V+=0. Con esto nuestro circuito se convierte en un circuito amplificador inversor, que ya conocemos y por tanto podemos decir que
-Segundo caso: V1=0:
Ahora el circuito es un amplificador NO inversor con la única diferencia de que en nuestro caso no aplicamos una tensión directamente sobre V+. Por ello, debemos buscar primero el valor de V+. Como sabemos que I=0, por lo tanto  .
.
sustituyendo en la expresión de Vo del amplificador NO inversor que ya conocemos obtenemos: ![]() .
.
La expresión de V0Total aplicando el teorema de superposición será:
En cuanto a la ganancia G será: ![]() .
.
Las expresiones que hemos obtenido anteriormente se deben en parte al hecho de disponer de dos resistencias R1 exactamente iguales entre sí y lo mismo ocurre con las R2. Por ello se dice que las R1 deben estar apareadas así como las dos resistencias R2, lo que quiere decir que deben ser exactamente iguales. Un tema importante a tener en cuenta en la utilización de este dispositivo es el de la impedancia que ofrece al exterior. Así, si colocamos los extremos de una pila en las entradas del circuito, debe de producir en la salida una señal amplificada de la entrada. Sin embargo esto no siempre es así.
En la figura de la izquierda mostramos cómo se conectaría la pila al circuito y a la derecha se muestra el esquema correspondiente formado por la pila ideal, una resistencia interna de la misma R0 y la resistencia de entrada Ri que muestra nuestro circuito al exterior. En caso de que R0 sea comparable a Ri caerá una tensión importante en los extremos de
R0 y la tensión en los extremos de Ri (la que el circuito tomará como señal de entrada) será muy diferente de la nominal de la pila. Por el contrario en el caso de que R0 sea muy pequeña frente a Ri casi toda la tensión caerá en Ri y por tanto se parecerá mucho a la tensión nominal de la pila. Vamos a calcular la resistencia de entrada de nuestro circuito.
Estudiando la malla señalada en la figura:
en donde el término (V–-V+) es nulo al considerar el caso ideal.
La resistencia de entrada será:
expresión que nos indica que nuestra resistencia de entrada no debe ser muy elevada. Si recordamos que G=R2/R1 y suponemos que G es muy grande, realmente estamos diciendo que R2 debe ser muy grande con respecto a R1 pero eso no indica que R1 sea grande. En muchos casos R1 puede alcanzar valores de 103 , 104e incluso más pero esos valores no son desde luego infinito. Para evitar los problemas presentados arriba y que nuestro circuito siga funcionando como se pretende colocamos un SEGUIDOR DE TENSIÓN a cada una de las entradas de nuestro circuito, como se muestra en la figura siguiente.
Dado que la intensidad de entrada en los dos seguidores de tensión es nula, la impedancia de entrada que ofrece el circuito será infinita. Este tipo de amplificadores forman la base principal de los amplificadores utilizados en los instrumentos de medidas.